Berikut ini adalah pembahasan tentang volume prisma, rumus volume prisma, contoh soal volume prisma, rumus volume prisma segitiga.
Untuk menentukan rumus umum volume sebuah prisma, marilah kita tinjau rumus volume prisma segitiga. Rumus volume prisma segitiga dapat diturunkan dari rumus volume balok. Perhatikanlah gambar berikut ini.
Jika balok ABCD.EFGH pada gambar (a) dibagi dua melalui bidang diagonal ACGE, maka akan diperoleh dua buah prisma segitiga, yaitu prisma ACD.EGH dan prisma ABC.EFG.
Karena bidang diagonal balok membagi balok menjadi dua bagian sama besar, maka volume balok sama dengan dua kali volume prisma segitiga. Maka volume prisma segitiga dapat dirumuskan:
Volume prisma segitiga = 12 × volume balok ABCD.EFGH
= 12 × AB × BC × CG
= 12 × luas bidang ABCD × CG
= 12 × (luas ΔABC + luas ΔACD) × CG
= 12 × (2 × luas ΔABC) × CG
= luas ΔABC × CG
= luas alas × tinggi prisma
Apakah untuk menentukan rumus volume prisma yang lain dapat menggunakan rumus volume prisma segitiga? Perhatikan gambar di bawah ini!
Jika prisma segienam beraturan kita iris pada bidang diagonal ADJG, bidang diagonal BEKH, dan bidang diagonal CFLI, maka kita akan mendapatkan enam buah prisma segitiga beraturan. Maka volume prisma segienam dapat dinyatakan dalam bentuk berikut.
Volume prisma segienam ABDEF.GHIJKL
= 6 × volume prisma segitiga BCO.HIT
= 6 × luas BCO × TO
= luas segienam ABCDEF × TO
= luas alas × tinggi prisma


Penyelesaian:
Sebelum mencari volume prisma, kita harus mencari luas alas prisma tersebut.
2a = 20 – 12 = 8
a = 4 cm
t = √52 – 42
= √25 – 16
= √9
= 3 cm
Luas alas = (20 + 12):2 × 3
= 32:2 × 3
= 16 × 3
= 48 cm2
Jadi, volume prisma adalah:
V = luas alas × tinggi prisma
= 48 × 25
= 1.200 cm3.
Baca juga: Rumus Luas Permukaan Limas
Volume Prisma
Volume merupakan isi dari suatu bangun ruang. Volume bangun ruang dapat ditentukan dengan menggunakan rumus.Untuk menentukan rumus umum volume sebuah prisma, marilah kita tinjau rumus volume prisma segitiga. Rumus volume prisma segitiga dapat diturunkan dari rumus volume balok. Perhatikanlah gambar berikut ini.
 |
| Gambar: Prisma Segi Empat |
Jika balok ABCD.EFGH pada gambar (a) dibagi dua melalui bidang diagonal ACGE, maka akan diperoleh dua buah prisma segitiga, yaitu prisma ACD.EGH dan prisma ABC.EFG.
Karena bidang diagonal balok membagi balok menjadi dua bagian sama besar, maka volume balok sama dengan dua kali volume prisma segitiga. Maka volume prisma segitiga dapat dirumuskan:
Volume prisma segitiga = 12 × volume balok ABCD.EFGH
= 12 × AB × BC × CG
= 12 × luas bidang ABCD × CG
= 12 × (luas ΔABC + luas ΔACD) × CG
= 12 × (2 × luas ΔABC) × CG
= luas ΔABC × CG
= luas alas × tinggi prisma
Apakah untuk menentukan rumus volume prisma yang lain dapat menggunakan rumus volume prisma segitiga? Perhatikan gambar di bawah ini!
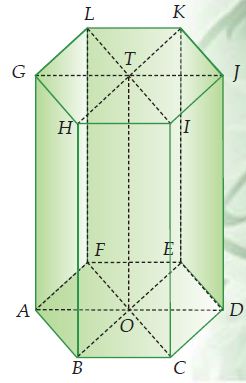 |
| Gambar: Prisma Segi Enam |
Jika prisma segienam beraturan kita iris pada bidang diagonal ADJG, bidang diagonal BEKH, dan bidang diagonal CFLI, maka kita akan mendapatkan enam buah prisma segitiga beraturan. Maka volume prisma segienam dapat dinyatakan dalam bentuk berikut.
Volume prisma segienam ABDEF.GHIJKL
= 6 × volume prisma segitiga BCO.HIT
= 6 × luas BCO × TO
= luas segienam ABCDEF × TO
= luas alas × tinggi prisma
Rumus Volume Prisma
Maka untuk setiap prisma berlaku rumus:
Contoh Soal Volume Prisma
Alas sebuah prisma berbentuk trapesium sama kaki dengan panjang sisi-sisi sejajarnya adalah 12 cm dan 20 cm, serta sisi miringnya 5 cm. Jika tinggi prisma tersebut 25 cm, hitunglah volume prisma!
Penyelesaian:
Sebelum mencari volume prisma, kita harus mencari luas alas prisma tersebut.
2a = 20 – 12 = 8
a = 4 cm
t = √52 – 42
= √25 – 16
= √9
= 3 cm
Luas alas = (20 + 12):2 × 3
= 32:2 × 3
= 16 × 3
= 48 cm2
Jadi, volume prisma adalah:
V = luas alas × tinggi prisma
= 48 × 25
= 1.200 cm3.
Baca juga: Rumus Luas Permukaan Limas